SEMANA 30: TALLER 19: CLASIFICACIÓN DE LOS CUADRILÁTEROS, LA CIRCUNFERENCIA, POLÍGONOS REGULARES---PLANO CARTESIANO

 

¿Qué es un cuadrilátero?   Ver video: clic

¿Qué es un Cuadrilátero?

Un cuadrilátero es una figura geométrica plana y cerrada que tiene:

• Cuatro lados

• Cuatro vértices

• Cuatro ángulos internos, cuya suma siempre es 360°

---

Clasificación de los Cuadriláteros

Los cuadriláteros se clasifican en tres grandes grupos:

1. Paralelogramos

Tienen dos pares de lados opuestos paralelos.

Incluye:

• Cuadrado

• Rectángulo

• Rombo

• Romboide

---

2. Trapecios

Tienen solo un par de lados opuestos paralelos.

Incluye:

• Trapecio rectángulo

• Trapecio isósceles

• Trapecio escaleno

---

3. Trapezoides

Ningún lado es paralelo.

---

1. PARALELOGRAMOS

---

🔷 CUADRADO

Características:

• 4 lados iguales

• 4 ángulos rectos (90°)

• Lados opuestos paralelos

Fórmulas:

• Área = L²

• Perímetro = 4 × L

Ejemplo:

Lado = 5 cm
Área = 5² = 25 cm²
Perímetro = 4 × 5 = 20 cm

🟦 RECTÁNGULO

Características:

• Lados opuestos iguales

• 4 ángulos interiores son iguales y rectos

• Lados adyacentes no iguales

Fórmulas:

• Área = base × altura

• Perímetro = 2 × (base + altura)

Ejemplo:

Base = 8 cm, altura = 3 cm
Área = 8 × 3 = 24 cm²
Perímetro = 2 × (8 + 3) = 22 cm

🟥 ROMBO

Características:

• 4 lados iguales

• Ángulos opuestos iguales

• Diagonales perpendiculares

• No todos los ángulos son rectos

Fórmulas:

• Área = (D × d) / 2

• Perímetro = 4 × L

Ejemplo:

Lado = 6 cm, D = 10 cm, d = 8 cm
Área = (10 × 8) / 2 = 40 cm²
Perímetro = 4 × 6 = 24 cm

🟩 ROMBOIDE (Paralelogramo no regular)

Características:

• Lados opuestos iguales y paralelos de 2 e 2.

• Ángulos opuestos iguales

• Sus lados contiguos son desiguales.

Fórmulas:

• Área = base × altura

• Perímetro = 2 × (base + lado oblicuo)

Ejemplo:

Base = 7 cm, altura = 4 cm, lado oblicuo = 5 cm
Área = 7 × 4 = 28 cm²
Perímetro = 2 × (7 + 5) = 24 cm

Gráfico:

  A-------B
 /         \
D-----------C

---

2. TRAPECIOS

---

🔺 TRAPECIO

Características:

• Solo un par de lados opuestos son paralelos

• Puede tener lados o ángulos iguales (depende del tipo)

Tipos:

• Trapecio rectángulo: un ángulo de 90°

• Trapecio isósceles: lados no paralelos iguales

• Trapecio escaleno: todos los lados diferentes

Fórmulas (para cualquier trapecio):

• Área = ((B + b) × h) / 2
  (B = base mayor, b = base menor, h = altura)

• Perímetro = suma de los 4 lados

Ejemplo:

B = 10 cm, b = 6 cm, h = 4 cm, lados no paralelos = 5 cm y 5 cm
Área = ((10 + 6) × 4) / 2 = 32 cm²
Perímetro = 10 + 6 + 5 + 5 = 26 cm

Gráfico:

   A------B
  /        \
 /          \
D------------C

---

3. TRAPEZOIDES

---

🟨 TRAPEZOIDE

Características:

• Ningún lado es paralelo

• Todos los lados y ángulos son diferentes

• Figura completamente irregular

Fórmulas:

• Área: requiere métodos especiales (Herón o coordenadas)

• Perímetro = suma de los 4 lados

Ejemplo:

Lados: 6 cm, 7 cm, 5 cm, 8 cm
Perímetro = 6 + 7 + 5 + 8 = 26 cm
Área: no se puede calcular sin más datos

Gráfico:

   A-----B
  /       \
 /         \
D-----------C

¿Qué es un Círculo?

Un círculo es una figura plana y cerrada formada por todos los puntos que están a la misma distancia de un punto llamado centro.

Partes del Círculo

• Centro: punto central

• Radio (r): distancia del centro al borde

• Diámetro (d): d = 2 × r

• Circunferencia: línea curva del borde

• Área: superficie encerrada por la circunferencia

---

Fórmulas

• Área = π × r²

• Perímetro (circunferencia) = 2 × π × r
  (π ≈ 3.1416)

---

Ejemplo

Radio = 5 cm

• Área = π × 5² = 3.1416 × 25 = 78.54 cm²

• Perímetro = 2 × π × 5 = 31.42 cm

Los cuadrados son los únicos cuadriláteros regulares (lados y ángulos iguales).

Debido a sus características comunes, se puede decir que el cuadrado es un rombo y un rectángulo y que los tres son romboides.

En este dibujo lo vas a entender mejor:

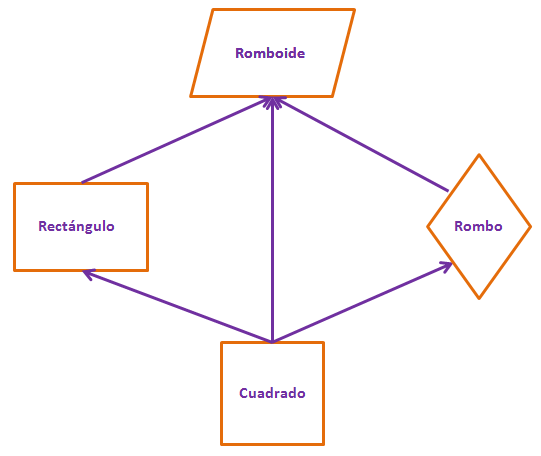
• El rectángulo es romboide.
• El rombo es romboide.
• El cuadrado es rectángulo, rombo y romboide.
• 
  

TALLER 19

Tema: cuadriláteros.

1. Realiza un mapa conceptual en tu cuaderno sobre los cuadriláteros, incluyendo:

• Su definición

• Clasificación (Paralelogramos, Trapecios y Trapezoides)

• Figuras que pertenecen a cada grupo

• Una imagen o dibujo de cada figura

• Fórmulas básicas de área y perímetro

Puedes usar colores y tu creatividad para organizar la información.

2. Cálculo de áreas en situaciones reales. Aplica las fórmulas de área para resolver los siguientes problemas cotidianos con procedimientos completos y gráfica en cada caso.

1. El patio del colegio tiene forma rectangular y mide 20 metros de largo por 12 metros de ancho.
   ¿Cuál es el área total del patio?
   👉 R: _____________________________________________

2. Una señal de tránsito en forma de rombo tiene una diagonal mayor de 80 cm y una diagonal menor de 60 cm.
   ¿Cuál es el área de la señal?
   👉 R: _____________________________________________

3. Un jardinero siembra flores en una zona con forma de trapecio, cuya base mayor mide 6 m, base menor 4 m y la altura 3 m.
   ¿Cuál es el área sembrada?
   👉 R: _____________________________________________