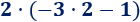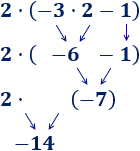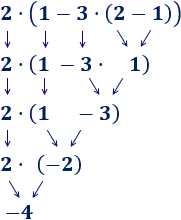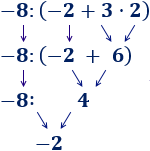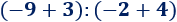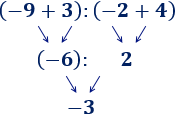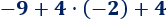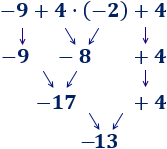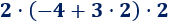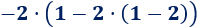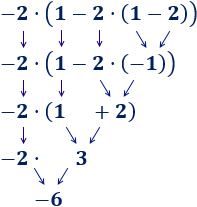16 AL 20 FEBRERO.
Para multiplicar dos números enteros se siguen estos pasos.
1. Se multiplican sus valores absolutos (en la práctica, los números entre sí).
2. Al resultado le colocamos el signo + si ambos números son de igual signo,
y el signo −si son de signos diferentes.
DIVISIÓN DE NÚMEROS ENTEROS
Para dividir dos números enteros se siguen estos pasos.
1. Se dividen sus valores absolutos (en la práctica, los números entre sí y
siempre que la división sea exacta).
2. Al resultado le colocamos el signo + si ambos números son de igual signo,
y el signo −si son de signos diferentes.
Ejemplos
Veamos los ejemplos que hemos preparado de la regla de los signos:
Para agilizar las operaciones de multiplicación y división de números enteros se
utiliza la regla de los signos:
Multiplicación División
(+) ⋅(+) = + (+) : (+) = +
(−) ⋅(−) = + (−) : (−) = +
(+) ⋅(−) = − (+) : (−) = −
(−) ⋅(+) = − (−) : (+) = −
Por ejemplo:
a) (+5) ⋅ (−3) = −15
b) (−5) ⋅ (−3) = +15
c) (+5) ⋅ (+3) = +15
d) 5 ⋅ 3 = 15
e) (+20) : (−4) = −5
f) (−20) : (−4) = +5
g) (+20) : (+4) = +5
h) 20 : 4 = 5
El producto de dos números enteros de igual signo es un número positivo.
5 × 4 = 20 −7 × (−2) = +14
El producto de dos números enteros de distinto signo es un número negativo.
8 × (−7) = −56 (−9) × 2 = −18
El cociente de dos números de igual signo es un número positivo.
21 ÷ 7 = 3 −16 ÷ (−2) = 8
El cociente de dos números de distinto signo es un número negativo.
60 ÷ (−12) = −5 −15 ÷ 5 = −3
Operaciones combinadas con números enteros
Las operaciones combinadas o mixtas son operaciones compuestas por varias
operaciones (sumas, restas, multiplicaciones y/o divisiones).
En estas operaciones, la multiplicación y la división tienen prioridad sobre la suma
y la resta. Los paréntesis pueden utilizarse para cambiar este orden.
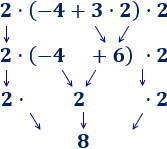
Ejemplo 1
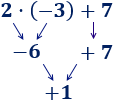
Hemos calculado la multiplicación y, después, la suma.
Ejemplo 2
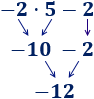
Hemos calculado la multiplicación y, después, la suma.
Ejemplo 3
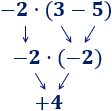
En esta operación, hemos calculado primero la resta porque había un paréntesis: El −2−2 multiplica al resultado de la resta del paréntesis.
Ejemplo 4
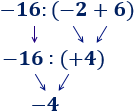
En esta operación, hemos calculado primero la suma porque había un paréntesis: el −16−16 tiene que dividirse entre el resultado de la suma del
paréntesis.
Ejercicios resueltos: operaciones combinadas
Ejercicio 1
Solución
Primero, calculamos la multiplicación:
Ejercicio 2
Solución
Primero, la resta del paréntesis:
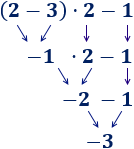
Ejercicio 3
Solución
Primero, la resta del paréntesis:
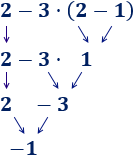
Observe que los números y operaciones de los 3 ejercicios anteriores son los mismos, pero los resultados son distintos porque los paréntesis cambian el orden de las operaciones.
Ejercicio 4
Solución
Primero, tenemos que resolver el paréntesis. Dentro de éste, tiene prioridad la multiplicación.
Ejercicio 5
Solución
Primero, la resta del paréntesis de dentro:
Ejercicio 6
Solución
Primero, la multiplicación del paréntesis:
Ejercicio 7
Solución
Primero, las sumas de los paréntesis:
Ejercicio 8
Solución
Primero, la multiplicación y, después, las sumas:
Ejercicio 9
Solución
Primero, la multiplicación del paréntesis y, seguidamente, la resta:
Ejercicio 10
Solución





















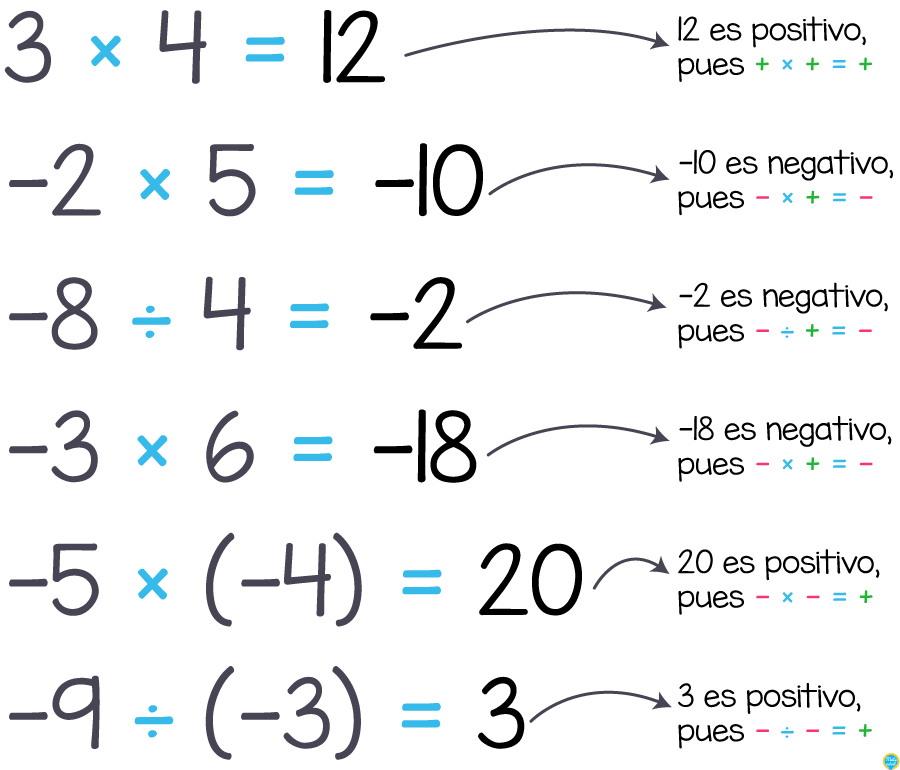
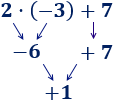 Hemos calculado la multiplicación y, después, la suma.
Hemos calculado la multiplicación y, después, la suma.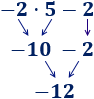 Hemos calculado la multiplicación y, después, la suma.
Hemos calculado la multiplicación y, después, la suma.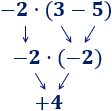 En esta operación, hemos calculado primero la resta porque había un paréntesis: El −2−2 multiplica al resultado de la resta del paréntesis.
En esta operación, hemos calculado primero la resta porque había un paréntesis: El −2−2 multiplica al resultado de la resta del paréntesis.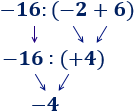 En esta operación, hemos calculado primero la suma porque había un paréntesis: el −16−16 tiene que dividirse entre el resultado de la suma del
En esta operación, hemos calculado primero la suma porque había un paréntesis: el −16−16 tiene que dividirse entre el resultado de la suma del
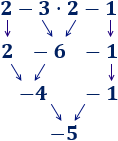
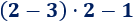
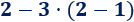
 Observe que los números y operaciones de los 3 ejercicios anteriores son los mismos, pero los resultados son distintos porque los paréntesis cambian el orden de las operaciones.
Observe que los números y operaciones de los 3 ejercicios anteriores son los mismos, pero los resultados son distintos porque los paréntesis cambian el orden de las operaciones.