Objetivo: Comprender y aplicar el concepto de porcentaje en situaciones cotidianas y matemáticas, utilizando estrategias como la regla de tres, fracciones y decimales, para resolver problemas prácticos y mejorar el razonamiento lógico-matemático.
Matemáticas grado 7° Año 2025
miércoles, 4 de junio de 2025
Semana 21. Taller 13: IVA y porcentaje
lunes, 2 de junio de 2025
SEMANA 19 y 20 TALLER 12: IVA, PORCENTAJE O TANTO POR CIENTO%
2 al 6 y 9 al 13 de junio
Ver video: Tipos de variables.
OBJETIVO
- Discriminar el valor de un producto y del IVA a partir del precio
- Calcular el porcentaje de un número dado.
Ejemplos:
- El 50% es la mitad del total (50 de cada 100).
- El 25% es la cuarta parte del total (25 de cada 100).
- El 20% es la quinta parte del total (20 de cada 100).
Ejemplo:
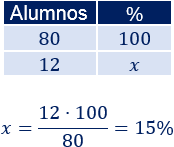
Cómo sacar un porcentaje con calculadora

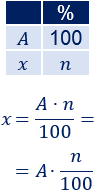 Como siempre realizamos la misma operación (multiplicar por n y dividir entre 100), podemos simplificar los cálculos multiplicando por el número decimal equivalente a la fracción n/100n/100.
Como siempre realizamos la misma operación (multiplicar por n y dividir entre 100), podemos simplificar los cálculos multiplicando por el número decimal equivalente a la fracción n/100n/100.Por ejemplo,
- La fracción
- 25
- /
- 100
- es 0,25 (al dividir entre 100, aparecen 2 decimales)
Por tanto, el 25% de 120 es 30
2) Calculamos el 30%
Tenemos que multiplicar por 0.30:
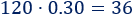
Entonces, si se debe pagar un servicio de $ 3966 + IVA, hay que calcular cuánto es el 19% de 3966.
domingo, 25 de mayo de 2025
SEMANA 18 Taller 11 : Variables ordinal, nominal, discreta y continua--Población, muestra e individuo
Objetivo:
Proporcionar al estudiante las herramientas estadísticas básicas que le permitirán plantear, resolver e interpretar problemas estadísticos reales
- El número de hermanos ( 1,2,3,4,5,etc.)
- El número de materias(1,2,3,4,etc.)
- La edad de los egresados de una carrera.
- La cantidad de mascotas que tienen los habitantes de una ciudad.
- La cantidad de animales que hay en las distintas reservas ecológicas de un país.
- La cantidad de ventas realizadas por cada empleado de una tienda.
- La cantidad de anotaciones que hacen los jugadores de baloncesto.
- La cantidad de panes que se fabrican cada día en una panadería.
- La estatura( puede ser: 1,20 m; 1,35m;1,80m;etc. )
- El tiempo( puede ser 2,30 h; 1,45h; 6,28h; etc. )
- El peso( puede ser 50, 38kg; 69, 30kg; 80,47kg; etc.)
- La altura que tienen los semáforos de una ciudad puede ser 10,51 m; 11,32 m; etc.
- El peso de los automóviles que se venden en un concesionario, cuyos valores pueden ser 1.308,78 kg; 1.774,98 kg; etc.
- El nivel educativo: secundario, bachillerato, universitario, etc.
- Estado económico( alto, medio, bajo)
- Satisfacción del cliente( insatisfecho, algo satisfecho, satisfecho, muy satisfecho y extremadamente satisfecho)
- Nivel educativo(preescolar, primaria, bachillerato, universidad)
- Calificaciones con letras( superior, alto, básico, bajo) etc.
- La profesión( ingeniero, médico, profesor, policía, chofer, etc.)
- Color de ojos( verdes, azules, miel, negros, cafés)
- Color de cabello( negro, castaño, rubio, rojo)
- Religión( católica, cristiana, evangélico)
- Estado civil( casado, soltero, divorciado, etc.
sábado, 17 de mayo de 2025
SEMANA 17 TALLER 10: Frecuencia relativa.
19 al 23 de mayo
Tema: Estadística descriptiva
sábado, 10 de mayo de 2025
Semana 16 Taller9 : estadística descriptiva: clases de variables.
12 AL 15 de mayo
Tema: Estadística descriptiva.
Conceptos básicos de estadística.
Taller # 9 Tema: Estadística descriptiva ver video
sábado, 26 de abril de 2025
SEMANA 15- TALLER DE RECUPERACION PARA ESTUDIANTES QUE NO ALCANZARON LOS LOGROS EN EL PRIMER PERÍODO.
ACTIVIDADES DE LA SEMANA: Repaso de diversos temas vistos durante el período.
Taller de recuperación primer
período 2024 grado séptimo _____
Nombre del
estudiante_________________________________________________________
Fecha________________________________________ Grado__________
Observaciones: Debe
realizar el taller en hojas de block con todos los procedimientos. Luego debe
estudiar muy bien el taller ya que se hará un examen escrito del mismo; también
debe ponerse al día en los cuadernos de matemáticas y geometría.
Tiene dos semanas a partir de la fecha de entrega del taller de recuperación.
1) Utiliza números enteros para
expresar el valor numérico de las siguientes afirmaciones:
a) Un helicóptero vuela a 4.500
metros de altura. B) Pitágoras
nació en el año 582 A.C
c) En la Antártida se registró
una temperatura de 12°c bajo cero.
d) Un pez se encuentra a una
profundidad de 6 metros de profundidad.
e) Me pagaron 460.000 pesos que
me debían.
2) Hallar el valor numérico de a+ b-c x (a – a - a + c)
Si a=-10; b= 5; c=-3. Recuerde hacer los procedimientos.
3) Resuelva paso a paso el
siguiente polinomio eliminando signos de agrupación:
{- 8+11- [-5 – 6 + 8 + (- 3 – 4 + 20) - (- 10 + 9 - 6)] + 18}
4) Resuelva las siguientes
multiplicaciones de números enteros:
a) -9 x (-2) x (-3) = b) 5 x (-3) x (-2) = c) -9 x (-5) x (-2) =
5) Resuelva las siguientes
divisiones de números enteros:
a)
(-100): (-50): (-2) = b) 90:
(-10): (-3) = c) -80: (-20):
2 =
6) Sume o reste números
enteros según el caso:
a)
-3-6-5-8= b) -7+8-3+9-15= c) 9+12-5-8+2+10 =
7) Empleando el
transportador, mida los siguientes ángulos y escriba su respectivo nombre de
acuerdo a su medida:
a) 43° b) 90° c) 250° d) 180° d) 192° e)360°
f) 113°
8) encuentre el
complemento o el suplemento de los siguientes ángulos:
a) 35° b) 92°
9) Calcule el área de los
siguientes triángulos: cuadriláteros (Hacer procedimientos completos y escribir
la fórmula en cada caso)
10) Hallar el área de los siguientes cuadriláteros (Hacer procedimientos completos y escribir la fórmula en cada caso)
viernes, 25 de abril de 2025
SEMANA 14 ---REPASO POTENCIACIÓN DE NÚMEROS ENTEROS---
TEMA: Repaso propiedades de la potenciación y seguimiento al taller número 8
Tema: Propiedades de la potenciación














