Potenciación con números enteros
Qué es una potencia de números enteros?
La potencia es la expresión abreviada de una multiplicación en que todos los factores son iguales.
an = a · a · a · … · a
El producto se hace n veces.
La base, a, es el factor que se repite.
El exponente, n, indica el número de veces que se repite la base.
La potencia es el resultado.
El exponente, n, indica el número de veces que se repite la base.
La potencia es el resultado.
Por ejemplo:
a) 24 = 2 · 2 · 2 · 2 = 16
b) 02 = 0 · 0 = 0
c) 40 = 1 (este es un caso especial, ya que no podemos multiplicar un número por sí mismo 0 veces)
d) 35 = 3 · 3 · 3 · 3 · 3 = 243
e) 19 = 1 · 1 · 1 · 1 · 1 · 1 · 1 · 1 · 1 = 1
Veamos que pasa cuando la base es un número negativo.
1) Si la base es negativa y el exponente es par, el resultado( potencia) es positivo.
Ejemplos:
(-3)2 = 9 porque (-3) . (-3) = 9
(-2)8 = 256 porque (-2) · (-2) · (-2) ·(- 2) ·(- 2) · (-2) · (-2) ·(- 2) = 256
2) Si la base es negativa y el exponente es impar, el resultado( potencia) es negativo.
Ejemplos:
(-3)3 =- 27 porque ( -3) . (-3) . (-3) = -27
(-2)9 = -512 porque (-2) · (-2) · (-2) ·(- 2) ·(- 2) · (-2) · (-2) ·(- 2) . (-2) = - 512
3) Si la base es positiva y el exponente es par o impar, el resultado( potencia) es positivo.
Ejemplos:
28 = 256 Porque 2 · 2 · 2 · 2 · 2 · 2 · 2 · 2 = 256
29 = 512 Porque 2 · 2 · 2 · 2 · 2 · 2 · 2 · 2. 2 = 512
4) Si la base es negativa y está elevada a un exponente par, pero esta base va fuera de un paréntesis, el resultado es negativo. Ejemplo:
-28 = - 2 ·- 2 · - 2 ·- 2 ·- 2 · - 2 · - 2 · - 2 = - 256
Pero, Si la base es negativa y está elevada a un exponente par, pero esta base va dentro de un paréntesis, el resultado es positivo. Ejemplo:
(-2)8 = (-2) · (-2) · (-2) ·(- 2) ·(- 2) · (-2) · (-2) ·(- 2) = 256
Como podes observar -28 no es igual a (-2)8
Aquí puedes ver que el exponente 8 es sólo para el número 2 y no para el signo menos(-), por ello el resultado es negativo. En cambio cuando escribimos -2 dentro del paréntesis y escribimos el exponente ocho tanto para la base como para el signo menos, dicho exponente afecta tanto al signo como al número.
DEBEMOS TENER EN CUENTA LAS SIGUIENTES REGLAS:
1) Las potencias de exponente par son siempre positivas.
(+)par = +
(−)par = +
2) Las potencias de exponente impar tienen el mismo signo de la base.
(+)impar = +
(−)impar = −
Propiedades de las potencias de números enteros
1) La potencia de exponente 0 es igual a 1:
Todo número elevado al exponente cero, es igual a 1. Ejemplo:
2) Potencia de base cero:
Ejemplo:
3) Exponente 1:
Todo número elevado al exponente 1, es igual a ese mismo número. Ejemplo:
4) Producto de potencias con la misma base:
Para multiplicar potencias que tengan igual base, escribimos la misma base y sumamos los exponentes. Ejemplo:
= 128
5) División de potencias con la misma base:
Para dividir potencias que tengan igual base, escribimos la misma base y restamos los exponentes. Ejemplo:
6) Potencia de exponente negativo:
7. Potencia de una potencia
8) Potencia de un producto: Sacamos las bases y las elevamos al exponente indicado, hallamos las potencias y multiplicamos. Llamada también distributiva de la multiplicación.
Resumamos:
PRIMERA FORMA: (−2 · 3)³
(−6)³= -216
SEGUNDA FORMA: (−2 · 3)³ =
-8 X 27 = −216
Sacamos las bases y las elevamos al exponente indicado, hallamos las potencias y multiplicamos.
9) Cociente de una potencia:
Sacamos las bases, las elevamos al exponente indicado, hallamos las potencias y dividimos.
RESUMAMOS:
PRIMERA FORMA: (−6 : 3)³ =
(-2)³ = -8
SEGUNDA FORMA:(−6 : 3)³ =
-216 : 27 = −8 Sacamos las bases y las elevamos al exponente indicado, hallamos las potencias y dividimos.
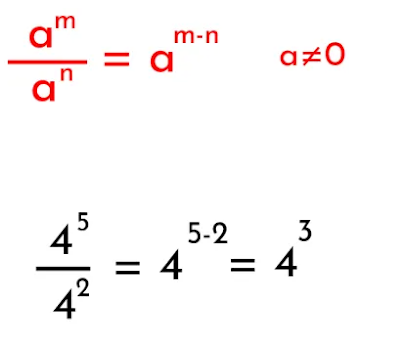
No hay comentarios:
Publicar un comentario