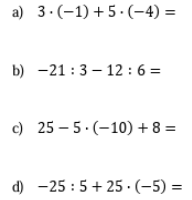ÁNGULOS.
jueves, 27 de febrero de 2025
SEMANA 7: TALLER 5: ÁNGULOS
miércoles, 19 de febrero de 2025
SEMANA 6. TALLER 4: Operaciones combinadas con números enteros.
24 febrero al 1 de marzo.
TALLER 4 TEMA: Operaciones combinadas con números enteros.
jueves, 6 de febrero de 2025
SEMANA 5 TALLER 3: MULTIPLICACIÓN Y DIVISIÓN DE NÚMEROS ENTEROS. TALLER 4: OPERACIONES COMBINADAS CON ENTEROS
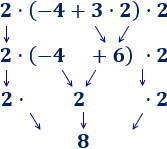
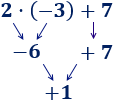 Hemos calculado la multiplicación y, después, la suma.
Hemos calculado la multiplicación y, después, la suma.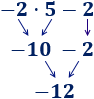 Hemos calculado la multiplicación y, después, la suma.
Hemos calculado la multiplicación y, después, la suma.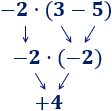 En esta operación, hemos calculado primero la resta porque había un paréntesis: El −2−2 multiplica al resultado de la resta del paréntesis.
En esta operación, hemos calculado primero la resta porque había un paréntesis: El −2−2 multiplica al resultado de la resta del paréntesis.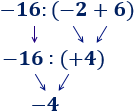 En esta operación, hemos calculado primero la suma porque había un paréntesis: el −16−16 tiene que dividirse entre el resultado de la suma del
En esta operación, hemos calculado primero la suma porque había un paréntesis: el −16−16 tiene que dividirse entre el resultado de la suma del
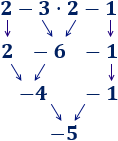
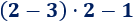
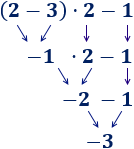
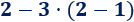
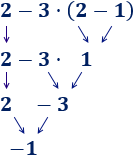 Observe que los números y operaciones de los 3 ejercicios anteriores son los mismos, pero los resultados son distintos porque los paréntesis cambian el orden de las operaciones.
Observe que los números y operaciones de los 3 ejercicios anteriores son los mismos, pero los resultados son distintos porque los paréntesis cambian el orden de las operaciones.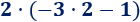
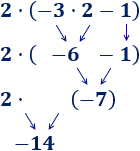

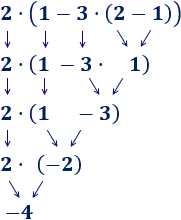

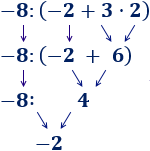
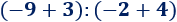
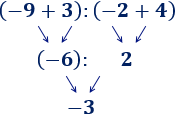
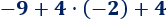
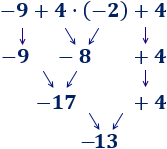
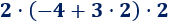
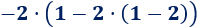
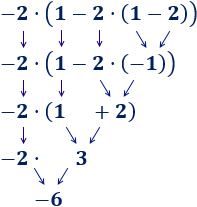
SEMANA 4. TALLER 2: VALOR ABSOLUTO, SUMA Y RESTA DE NÚMEROS ENTEROS.
FEBRERO 10 AL 14
ORDEN EN LOS NÚMEROS ENTEROS Y VALOR ABSOLUTO
Cuando resolvemos sumas y restas de números enteros, nos podemos encontrar con varias situaciones:
1.- Suma de números enteros
Vamos a distinguir tres casos:
a) Si todos los números son positivos se suman y el resultado es positivo:
3 + 4 + 8 = 15
b) Si todos los números son negativos se suman y el resultado es negativo:
(-3) + (-4) + (-8) = -15
c) Si se suman números positivos y negativos, los positivos suman y los negativos restan:
3 + (-4) + 5 + (-7)
Aparte sumamos los números positivos: 3 + 5 = 8
Aparte sumamos los números negativos: (-4) + (-7) = -11
Ahora el resultado positivo suma y el negativo resta:
8 - 11 = -3
¿Cómo a 8 le podemos restar 11? Ponemos como minuendo la cifra mayor (11) y como sustraendo la menor (8), pero el resultado toma cómo signo el de la cifra mayor (en este ejemplo toma el signo " - " porque 11 es negativo)
11 - 8 = 3
Pero le ponemos el signo " - ", luego el resultado es "-3"
2.- Resta de números enteros
Una resta de números enteros se puede resolver como si se tratara de una suma, pero con una particularidad:
El símbolo de la resta le cambia el signo a la cifra que le sigue, por lo que:
Si el número que se resta es positivo lo convierte en negativo.
Si el número que se resta es negativo lo convierte en positivo.
Vamos a ver a continuación cuatro posibles casos:
a) A un número positivo le restamos otro número positivo:
(+3) - (+2) = 3 - 2 = 1
b) A un número positivo le restamos un número negativo:
3 - (-4) Multiplico los dos signos que están seguidos
3 + 4= 7
c) A un número negativo le restamos otro número negativo:
(-3) - (-4) Multiplico los dos signos que están seguidos
(-3) + (4) Como son signos contrarios, entonces se resta
4 - 3 = 1 Al número mayor le restamos el menor
d) A un número negativo le restamos un número positivo:
(-3) - 4 como los dos tienen signos iguales, entonces se suman
(-3) + (-4)
Al el resultado se le pone el signo negativo: (-3) + (-4) = -7
Tomado de https://ele.chaco.gob.ar/mod/book/view.php?id=92398
Adición y Sustracción de números enteros.
Para sumar dos números enteros se procede de la siguiente forma:
1. Si los números tienen el mismo signo, se suman sus valores absolutos y se mantiene el signo común. Ejemplos:
a) 13 + 8 = 21 b) –3 + (–15) =- 3 - 15= –18
2. Si los números tienen diferente signo, se restan sus valores absolutos (el mayor menos el menor) y se coloca el signo del que tenga el mayor valor absoluto. Ejemplos:
a) –23 + 64 = (64 – 23) = 41 b) –37 + 5 = –32
TALLER N°2 Tema: Valor absoluto, suma y resta de números enteros.
1) Escriba al frente el valor absoluto
SEMANA TRES. TALLER 1. NÚMEROS ENTEROS
3 AL 7 DE FEBRERO
TALLER 1 TEMA: NÚMEROS ENTEROS
- La rueda 3500 ac
- La imprenta 1460 dc
- El papel 850 dc
- La pólvora 954 dc
- La bicicleta 1817 dc
- El computador 1941 dc
- La tinta 400 ac
- La polea 250 ac